CARLOS EDUARDO FALCONI

INTRODUÇÃO

Antes de iniciar este estudo, é preciso relembrar os conceitos de DLA (diferença de latitude) e DLO (diferença de longitude).

A primeira – DLA – é a diferença angular entre duas latitudes, podendo ser de no máximo 180 graus, pois é a diferença entre 90ºN e 90ºS.

A segunda – DLO – é a menor diferença angular entre duas longitudes, podendo ser, também, de no máximo 180 graus, pois é a diferença entre a longitude de um meridiano qualquer e seu anti-meridiano (oposto a ele em 180º).

Para se calcular a distância entre duas localidades apenas sabendo-se as coordenadas, precisaremos também lembrar como converter estes valores de DLA e DLO em distância.

Para se calcular a direção entre duas localidades será necessário relembrar conceitos de trigonometria, como veremos mais à frente.

TRANSFORMANDO UM VALOR DE DLA OU DLO EM DISTÂNCIA

Para transformar um valor angular em distância, basta relembrar suas equivalências.

Como se sabe, 1º = 60 NM, assim pode-se concluir que 60′ = 60 NM \ 1′ = 1 NM.

Ocorre que 1′ = 60″, assim pode-se concluir que 60″ = 1 NM, ou seja, 1″ = 1/60 NM.

Sabendo-se estas equivalências, fica fácil transformar qualquer valor de DLA ou DLO em distâncias. Observe o exemplo a seguir.

Vamos converter o valor 23º 30’ 36” em distância. Basta isolar cada valor e converter individualmente, somando os resultados.

23º  X 60 = 1.380

30’ X 1 = 30

36” ÷ 60 = 0,6

‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾

1.380 + 30 + 0,6  = 1.410,6 NM x 1,852 = 2.612,4 Km

Obviamente, este método vale para distâncias pequenas (menores do que 800 NM), pois o correto seria levar em conta a curvatura terrestre; no entanto, o método funciona muito bem, como veremos adiante.

CALCULANDO A DISTÂNCIA ENTRE DOIS PONTOS GEOGRÁFICOS

Pode ocorrer de, em determinado momento, o piloto ter as coordenadas entre dois pontos, mas não ter em mãos a carta ou algum equipamento para calcular a distância entre elas. Quando isto acontecer, basta utilizar o que já se conhece sobre coordenadas geográficas. Já foi visto que uma coordenada geográfica utiliza o sistema cartesiano para indicar localidades. Fazendo uma análise simples, qualquer coordenada pode ser representada em um sistema de eixos do tipo “x” e “y”.

Vamos pegar como exemplo as coordenadas geográficas das duas cabeceiras da pista de SBMT (Aeroporto Campo de Marte, São Paulo):

SBMT: PISTA 12 (23º 30’ 29,93” S/046º 38’ 32,90” W)

­SBMT: PISTA 30 (23º 30’ 36,50” S/046º 37’ 53,01” W)

Vamos agora calcular o comprimento da pista, utilizando as duas coordenadas.

Basta uma pequena análise para se perceber que o comprimento da pista é definido por uma linha que liga os dois pontos e que esta linha nada mais é do que a hipotenusa de um triângulo retângulo definido pelas diferenças de latitude (DLA) e de longitude (DLO), que são os catetos entre estes pontos. Veja o esquema abaixo:

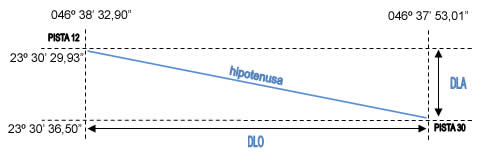
Pelo Teorema de Pitágoras, o quadrado da hipotenusa é igual à soma dos quadrados dos catetos. Podemos considerar que um dos catetos é a DLA e o outro a DLO, sendo a hipotenusa o comprimento da pista (ou a distância entre os dois pontos). Assim, valerá sempre a fórmula:

COMPRIMENTO ² = DLA ² + DLO ²

Vamos, então, calcular as DLA e DLO:

DLA = 23º 30’ 36,50” – 23º 30’ 29,93” = 6,57”

DLO = 046º 38’ 32,90” – 046º 37’ 53,01” = 39,89”

Sabendo o valor das DLA e DLO, basta transformá-las em distância, dividindo-as por 60:

DLA = 6,57” ÷ 60 = 0,1095 NM x 1.852 = 202,8 metros

DLO = 39,89” ÷ 60 = 0,6648 NM x 1.852 = 1.231,2 metros

Colocando-se os valores na fórmula:

COMPRIMENTO ² = 202,8 ² + 1.231,2 ² = raiz (41.127,84 + 1.515.853,44)

COMPRIMENTO = 1.247,8 metros

Para provar que o cálculo está correto, vamos utilizar a ferramenta régua do Google Earth:

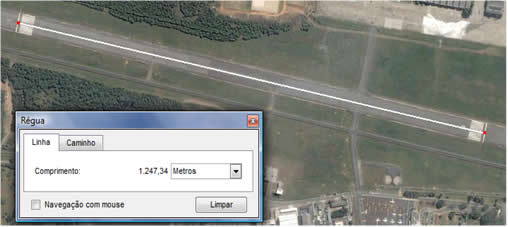
CALCULANDO A DIREÇÃO ENTRE DOIS PONTOS GEOGRÁFICOS

Até o momento, utilizou-se apenas uma calculadora simples para os cálculos, necessitando-se somente do valor de uma raiz quadrada.

Veremos agora que, apesar de um pouco complexo, há a possibilidade de se efetuar o cálculo da direção entre dois pontos geográficos. Para isso, será necessário rever conceitos de básicos de trigonometria e da teoria dos triângulos.

Como o triângulo que vamos estudar é um triângulo retângulo, teremos o seguinte desenho:

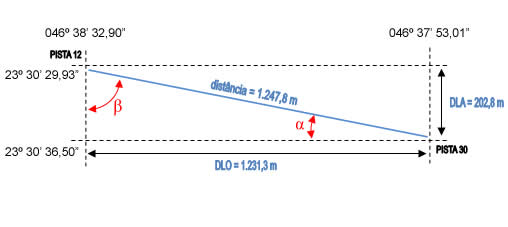
Pela teoria dos triângulos, a soma interna de todos os ângulos é sempre igual a 180º. Assim,

α + β + 90º = 180º

Basta, portanto, achar α para achar β ou vice-versa:

α  = 90º – β

β = 90º – α

Para calcular o valor dos ângulos, é necessário lembrar-se dos conceitos de trigonometria.

O valor de um ângulo em um triângulo retângulo pode ser assim calculado:

• Tangente de um ângulo é igual ao cateto oposto sobre o adjacente
• Seno de um ângulo é igual ao cateto oposto sobre a hipotenusa
• Cosseno de um ângulo é igual ao cateto adjacente sobre a hipotenusa

Sabendo-se disso, tomando-se por base o ângulo α , podemos deduzir que:

tan α  = DLA ÷ DLO

sen α  = DLA ÷ distância

cos α  = DLO ÷ distância

Uma vez que os valores de DLA e DLO são mais facilmente encontrados, vamos, então, aplicar estes valores utilizando a fórmula da tangente de α :

tang α  = 202,8 ÷ 1.231,3 = 0,1647

Sabendo-se o valor da tangente, basta calcular a tangente inversa, ou seja, o arco-tangente deste ângulo. O resultado desta operação, que deverá ser feita utilizando-se uma calculadora com esta função ou o Excel – como veremos a seguir – pode ser assim representado:

arctan α  = tan^-1 α

Esta operação dá o valor em radianos, os quais devem ser convertidos em graus.

Uma calculadora mais avançada faz este cálculo rapidamente, bastando clicar na função “inverso” e depois na função “graus/radianos”.

No Excel basta colocar a seguinte fórmula:

=graus(atan(tanα))

=graus(atan(DLA/DLO))

Aplicando esta fórmula no Excel, temos:

α = graus(atan(0,1647)), o resultado será 9,352651º, ou seja, arredondando-se para números inteiros, será 9º.

Se α = 9º, β = 90º – α \ β = 90º – 9º = 81º, ou seja:

α = 9º

β = 81º

É importante ressaltar que estes valores são da parte interna do triângulo, que ficará assim:

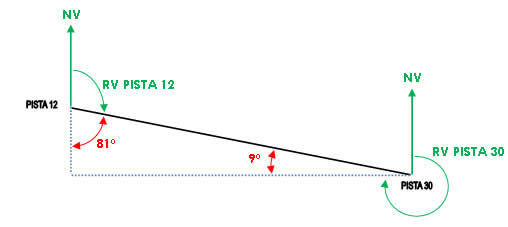
Portanto, os valores dos Rumos Verdadeiros (RV) das pistas 12 e 30 serão, respectivamente:

RV PISTA 12 = 180º – 81º = 99º

RV PISTA 30 = 270º + 9º = 279º

Como a declinação magnética do SBMT é 21ºW, os Rumos Magnéticos serão, respectivamente:

RM PISTA 12 = 99º + 21º = 120º

RM PISTA 30 = 279º + 21º = 300º

Isto prova que os cálculos estão corretos, pois senão as pistas não seriam 12 e 30.